شماره تلفن!

1) هفت رقم شماره ی تلفن خود را در نظربگیرید.

2)حالا سه رقم اول آن را وارد ماشین حساب کنید.یعنی اگر تلفن شما ۱۲۳۴۵۶۷ باشد ۱۲۳ را در ماشین حساب وارد کنید.

3) حالا این سه رقم را در ۸۰ ضرب کنید و حاصل را با ۱ جمع کنید.

4) عدد به دست آمده را در ۲۵۰ ضرب کنید.

5) حالا چهار رقم پایانی تلفن خود رابا عدد به دست آمده جمع کنید. یک بار دیگر چهار رقم پایانی شماره ی خود را با آن جمع کنید.

6) عدد ۲۵۰ را از حاصل به دست آمده کم کنید.

7) حالا حاصل را تقسیم بر ۲ کنید

آیا این شماره برای شما آشنا نیست؟

با تشکر از سرکار خانم اخوان

سوالی برای دانش‌آموزان مقطع راهنمایی

سئوال

چهار عدد صحيح ونامنفی دلخواه، مثلا 47، 55، 17، 25 را روی دايره‌‌‌‌‌‌‌‌ای بنويسيد

سپس از هر دو عدد مجاور عدد کوچکتر را از عدد بزرگتر کم کنيد

و چهار عدد حاصل را روی دايره بعدی قرار دهيد و چهارتائی بعدی را بدست آوريد و...

الف- به نظر شما چه اتفاقی می‌افتد؟

ب- آيا اين پديده برای هر پنج عدد دلخواه هم برقرار است؟

در هر حالت مشاهده خود را بيان کنيد و سعی کنيد نتيجه حاصل را حدس و سپس اثبات کنيد.

پاسخ یکی از کاربران محترم و ارائه یک الگوی اثبات جبری در ادامه ی مطلب

ادامه نوشته

1089

یك عدد سه رقمي انتخاب كنيد كه يكان وصدگان آن حداقل دو واحد اختلاف داشته باشد.

مثال اول:       157

مقلوب اين عدد را بنويسيد.        751

اختلاف عدد و مقلوبش را بدست آوريد.         594=157-751

اكنون عدد حاصل (در اين مثال: 594) را با مقلوبش جمع كنيد.       1089=495+594

پاسخ بدست آمده يك عدد چهار رقمي است.       "۱۰۸۹"

مثال دوم:    

مرحله اول:      

عدد انتخابي:        905

 مرحله دوم:           396=509-905

مرحله سوم:          1089=693+396

در مثال دومي نيز عدد  1089 بدست آمد.

آيا شما نيز با انتخاب یک عدد دلخواه و طی این روند ساده به همين عدد خواهيد رسيد؟ امتحان كنيد.

و اگر پاسخ مثبت است. چرا بايد به عدد 1089 برسيم؟

ادامه نوشته

یه سؤال جالب و یک راه حل فوق العاده !

ليوويل رياضي دان فرانسوي اين مسئله را در برابر خود گذاشت كه:

عدد هاي دلخواه a   و b  و c  و . . .  چگونه باشند تا مجموع مكعب هاي آنها مساوي مجذور مجموع آنها باشد.

 

يا به عبارتي ديگر   a   و b  و c  و . . .  چگونه باشند تا:

   

 

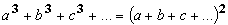
ليوويل توانست  يك جواب خيره كننده براي اين مسئله بدست آورد.

 عدد هاي مورد نظر " تعداد مقسوم عليه هاي هر يك از تمام مقسوم عليه هاي يك عدد دلخواه است"

 

مثال:عدد 6 را در نظر بگيريد.

 

 اين عدد بر يك و دو و سه و شش بخش پذير است.

 

عدد يك داراي (1) مقسوم عليه و عدد دو داراي (2) مقسوم عليه

و عدد سه داراي (2)  مقسوم عليه و  عدد شش داراي (4) مقسوم عليه مي باشد.

 

بنابراين همين تعداد مقسوم عليه ها يعني 1 و 2 و 2 و 4 در رابطه مورد نظر صدق مي كند.

 

 ²(4+2+2+1)=4³+2³+2³+1³   

 

          9²=64+8+8+1

---

(*)در صورتی که عدد 2^n-1 را در نظر بگیریم. تمام مقسوم علیه های آن عبارتند از:

1  ,  2  ,  2²   ,   2³   ,   2⁴   ,    2⁵    ,    2⁶    ,    .   .   .  ,  2^n-1

و تعداد مقسوم علیه های هر یک به ترتیب:

1  ,   2  ,  3   ,    4   ,    5   ,    6    ,       7    ,   .   .   .   ,  n     خواهد شد

و یکی از حالت های خاص چنین خواهد بود: 

1³+2³+3³n+. . . +n³)=(1+2+3n+. . . +n)²)

مثال:

1³+2³+3³n+4³)=(1+2+3n+4)²)

10²=1+8+27+64

یک نکته ی جالب

عدد 13837 را در سن خودتون ضرب کنید حالا حاصلش رو در 73 ضرب کنید! حاصل چه می شود؟

با تشکر از دانش آموز خوبم سجاد سلطان پور

اول یا مرکب

يكي از دانش آموزان خوبم ، آدرس سايتي رو برايم ارسال كرده ، كه مي توانيم از آن براي

 تشخيص اول يا مركب بودن اعداد طبيعي استفاده كنيم.

ابتدا بايد ،در كادر Number to Check عدد مورد نظر را وارد كنيم،

و با كليك كردن در كادر Result نتيجه را خواهيم ديد.

اگر آن عدد مركب باشد ، عدد را به صورت حاصل ضرب دو عدد طبيعي خواهد نوشت.

واگر عدد مورد نظزعددي اول باشد پیام" is prime" ظاهر خواهد شد.

براي تعيين اول بودن يا مركب بودن يك عدد طبيعي اينجا كليك كنيد.

UP

اول يا مركب

يكي از دانش آموزان خوبم ، آدرس سايتي رو برايم ارسال كرده ، كه مي توانيم از آن براي

 تشخيص اول يا مركب بودن اعداد طبيعي استفاده كنيم.

ابتدا بايد ،در كادر Number to Check عدد مورد نظر را وارد كنيم،

و با كليك كردن در كادر Result نتيجه را خواهيم ديد.

اگر آن عدد مركب باشد ، عدد را به صورت حاصل ضرب دو عدد طبيعي خواهد نوشت.

واگر عدد مورد نظزعددي اول باشد پیام" is prime" ظاهر خواهد شد.

براي تعيين اول بودن يا مركب بودن يك عدد طبيعي اينجا كليك كنيد.

UP

رمز و راز اعداد

در ميان عددهاي طبيعي مي توان دسته اي از عددها پيدا كرد كه با دسته اي از

 عددهاي ديگر ارتباطي معنا دار دارد.

و بعضا يك دسته از عددها با دسته اي ديگر آنچنان درهم تنيده اند، كه انسان را به

حيرت وا مي دارد.كه گويا اين عددها خود گواه بارزي از زيبايي و نظم و اعجازند.

به اين نمونه ها دقت كنيد:     

درمورد   ۲،۳،۷  و ۱،۵،۶

                ۶+۵+۱=۷+۳+۲

           ۶^۲+۵^۲+۱^۲=۷^۲+۳^۲+۲^۲

در مورد ۹،۸،۲،۱ و ۱۰،۵،۵

           ۹+۸+۲+۱=۱۰+۵+۵

     ۹^۲+۸^۲+۲^۲+۱^۲=۱۰^۲+۵^۲+۵^۲

     ۹^۳+۸^۳+۲^۳+۱^۳=۱۰^۳+۵^۳+۵^۳

و براي شش عدد ۱،۶،۷،۱۷،۱۸،۲۳ در برابر شش عدد ۲،۳،۱۱،۱۳،۲۱،۲۲

۲۲+۲۱+۱۳+۱۱+۳+۲=۲۳+۱۸+۱۷+۷+۶+۱

۲۲^۲+۲۱^۲+۱۳^۲+۱۱^۲+۳^۲+۲^۲=۲۳^۲+۱۸^۲+۱۷^۲+۷^۲+۶^۲+۱^۲

۲۲^۳+۲۱^۳+۱۳^۳+۱۱^۳+۳^۳+۲^۳=۲۳^۳+۱۸^۳+۱۷^۳+۷^۳+۶^۳+۱^۳

۲۲^۴+۲۱^۴+۱۳^۴+۱۱^۴+۳^۴+۲^۴=۲۳^۴+۱۸^۴+۱۷^۴+۷^۴+۶^۴+۱^۴

۲۲^۵+۲۱^۵+۱۳^۵+۱۱^۵+۳^۵+۲^۵=۲۳^۵+۱۸^۵+۱۷^۵+۷^۵+۶^۵+۱^۵

"مثال هاي ديگري نيز با يك چنين روابطي يافت مي شود"

1089

یك عدد سه رقمي انتخاب كنيد كه يكان وصدگان آن حداقل دو واحد اختلاف داشته باشد.

مثال اول:       157

مقلوب اين عدد را بنويسيد.        751

اختلاف عدد و مقلوبش را بدست آوريد.         594=157-751

اكنون عدد حاصل (در اين مثال: 594) را با مقلوبش جمع كنيد.       1089=495+594

پاسخ بدست آمده يك عدد چهار رقمي است.       "۱۰۸۹"

مثال دوم:    

مرحله اول:      

عدد انتخابي:        905

 مرحله دوم:           396=509-905

مرحله سوم:          1089=693+396

در مثال دومي نيز عدد  1089 بدست آمد.

آيا شما نيز با انتخاب یک عدد دلخواه و طی این روند ساده به همين عدد خواهيد رسيد؟ امتحان كنيد.

و اگر پاسخ مثبت است. چرا بايد به عدد 1089 برسيم؟پاسخ در ادامه ی مطلب!

ادامه نوشته

9

نقش منحصر به فرد عدد ۹ در برج های عددی زیبا و باشکوه

11=2+9×1

222=33+9×21

3333=444+9×321

44444=5555+9×4321

555555=66666+9×54321

6666666=777777+9×654321

77777777=8888888+9×7654321

888888888=99999999+9×87654321

 

1=1+9×0

11=2+9×1

111=3+9×12

1111=4+9×123

11111=5+9×1234

111111=6+9×12345

1111111=7+9×123456

11111111=8+9×1234567

111111111=9+9×12345678

1111111111=10+9×123456789

16

مي دانيم كه: عدد 16 مجذور كامل است.            4²=16

اگر بين رقم هاي 1و6 رقم 15 را قرار دهيم. عدد 1156 ايجاد خواهد شد كه : 34²=1156

دوباره  رقم 15 را وسط رقم هاي 1156 قرار دهيم. به عدد 111556 مي رسيم،

 كه باز هم مجذور كامل است.                 334²=111556

 به نظر مي زسد كه هر چه اين عمل را تكرار كنيم. و عدد 15 را در مركز عدد قبلي

بگذاريم، مجذور بودن آن، از بين نمي رود!  ۴²=16

    34²=1156

    334²=111556

    3334²=111۱۵556

    33334²=1111155556

    333334²=111111555556

    3333334²=11111115555556

جالب است بدانيد كه : عدد ديگري مثل 16 وجود دارد كه داراي اين خاصيت است.

يعني: هر چند بار رقم هاي  a  و b-1   را در مركز (ab) قرار دهيم، باز هم،

 مجذور يك عدد صحيح باقي خواهد ماند.آن عدد را پيدا كنيد؟           

رمز و راز اعداد

5796=12×483                                    6952=4×1738

5346=18×297                                    7852=4×1963

4396=28×157                                    5346=27×198

7254=39×186                                    5796=42×138    

  به ضرب های بالا دقت كنيد.                                    

چه وجه مشتركي در اين ضرب ها مي بينيد؟

در صورت تمايل پاسخ را در ادامه مطلب ببينيد.

ادامه نوشته

6174

الف: يك عدد چهار رقمي بنويسيد."به نحوي كه همه رقم هاي آن يكي نباشد"

(تساوي بعضي رقم ها عيبي ندارد)

ب: از رقم هاي عددي كه نوشته ايد دو عدد تازه تشكيل دهيد.

(بزرگترين عدد ممكنM=  و كوچكترين عدد ممكنm=)

پ: r = M – m  را پيدا كنيد.(اگر  r چهار رقمي نبود يك صفر در سمت چپ آن قرار دهيد.)

  مراحل ب و پ را براي r   انجام دهيد

 "بالاخره به اختلاف 6174 مي رسيم كه بعد از آن هميشه همين عدد به عنوان تفاضل

تكرار مي شود!"

مثال: عدد انتخابي من : 4818

7353= r₁         7353=1488-8841         1488= m₁         8841= M₁

 4176= r₂        4176=3357-7533        3357= m₂          7533= M₂

6174= r₃         6174=1467-7641        1467= m₃          7641= M₃

6174= r₄        6174=1467-7641        1467= m₄          7641=M₄

آيا با انتخاب سال تولد تان نيز به اختلاف 6174 مي رسيد؟(امتحان كنيد)

 بین عددهای صحیح می توان زوج هایی پیدا کرد ،که:

  حاصل جمع و حاصل ضرب آنها   تنها در جای رقم هایشان   با هم   فرق دارند.

        ۸۱=۹×۹             ۱۸=۹+۹                   (۹و۹)

        ۷۲=۳×۲۴           ۲۷=۳+۲۴                (۳و۲۴)

          ۹۴=۲×۴۷          ۴۹=۲+۴۷                (۲و۴۷)

      ۵۲۶=۲×۲۶۳      ۲۶۵=۲+۲۶۳             (۲و۲۶۳)

         ۹۹۴=۲×۴۹۷     ۴۹۹=۲+۴۹۷             (۲و۴۹۷)

  این هم سه زوج از عددهای متوالی که مجذورهای آنها،در جای رقم ها

با هم فرق دارند.

   ۸۳۳۵۶۹=۹۱۳^۲              ۲۴۶۴۹=۱۵۷^۲               ۱۶۹=۱۳^{۲                              و                               و                           و}                          ۸۳۵۳۹۶=۹۱۴^۲               ۲۴۹۶۴=۱۵۸^۲                ۱۹۶=۱۴^۲

خاصیت اعداد فرد

                            ۱=۱^۳                       

                   ۵+۳=۲^۳           

             ۱۱+۹+۷=۳^۳                        

    ۱۹+۱۷+۱۵+۱۳=۴^۳    

    ۵^۳    را شما حدس بزنید .                    

      آیا  ۶^۳  را هم می توانید به شکل نمونه های بالا حدس بزنید؟ (امتحان کنید)                    

نكته هاي جالبي از اعداد

يك عدد شگفت انگيز:              ۱۴۲۸۵۷

اگر پی در پی رقم یکان عدد را برداشته و در سمت راست، قرار دهیم، داریم:

۱۴۲۸۵۷×۵=۷۱۴۲۸۵

۱۴۲۸۵۷×۴=۵۷۱۴۲۸

۱۴۲۸۵۷×۶=۸۵۷۱۴۲

۱۴۲۸۵۷×۲=۲۸۵۷۱۴

۱۴۲۸۵۷×۳=۴۲۸۵۷۱

---

 ^{و چند عدد جالب !}

^۲(۰۱+۹۸)=۹۰۸۱                                              ۳=۲+۱

 ^۲(۲۵+۳۰)=۳۰۲۵                                          ۸+۷=۶+۵+۴

 ۷^۳+۳^۳=(۷+۳)۳۷                                ۱۵+۱۴+۱۳=۱۲+۱۱+۱۰+۹              

 ۸^۳+۴^۳=(۸+۴)۴۸                        در هر تساوي ،عددي كه پر رنگ نوشته  شده

 ۷^۳+۱۴^۳=(۷+۱۴)۱۴۷                        برابر است با تعداد جمله هاي سمت چپ

 ۸^۳+۱۴^۳=(۸+۱۴)۱۴۸                         در تعداد جمله هاي سمت راست                   

۱^۳+۱۱^۳=(۱+۱۱)۱۱۱

---

بازی ، ریاضی و هوش!!!